1 You should express y first y = x 3 / 2 Then y ′ = 3 2 x 1 / 2 and ∫ 0 5 / 9 1 y ′ 2 d x = ∫ 0 5 / 9 1 9 4 x d x = 8 27 ( 1 9 4 x) 3 / 2 x = 0 x = 5 / 9 = 19 27 ShareThe process of obtaining the equation is similar, but it is more algebraically intensive Given the focus (h,k) and the directrix y=mxb, the equation for a parabola is (y mx b)^2 / (m^2 1) = (x h)^2 (y k)^2 Equivalently, you could put it in general form x^2 2mxy m^2 y^2 2 h (m^2 1) mbx 2 k (m^2 1)^2 by (h^2 k^2So the equation for the line of symmetry is x = 3 In order to visualize the line of symmetry, take the picture of the parabola above and draw an imaginary vertical line through the vertex

Characteristics Of Parabolas College Algebra
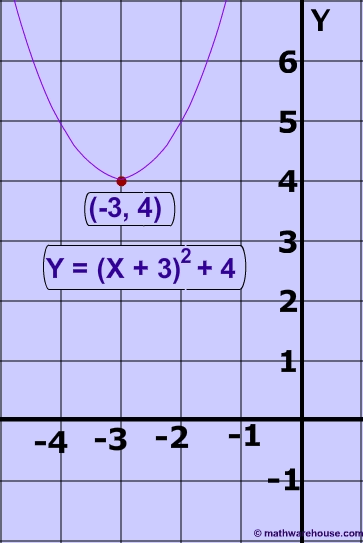
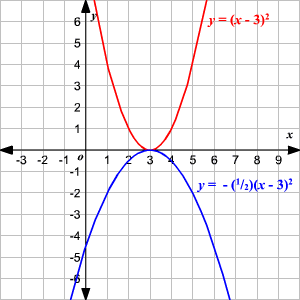
Vertex of parabola y=2(x-3)^2+4
Vertex of parabola y=2(x-3)^2+4- The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equationReleased under CC BYNCSA http//creativecommonsorg/licenses/byncsa/30/legalcode Graphing a basic parabola using y=(1/3)x^21 to show a negative consta
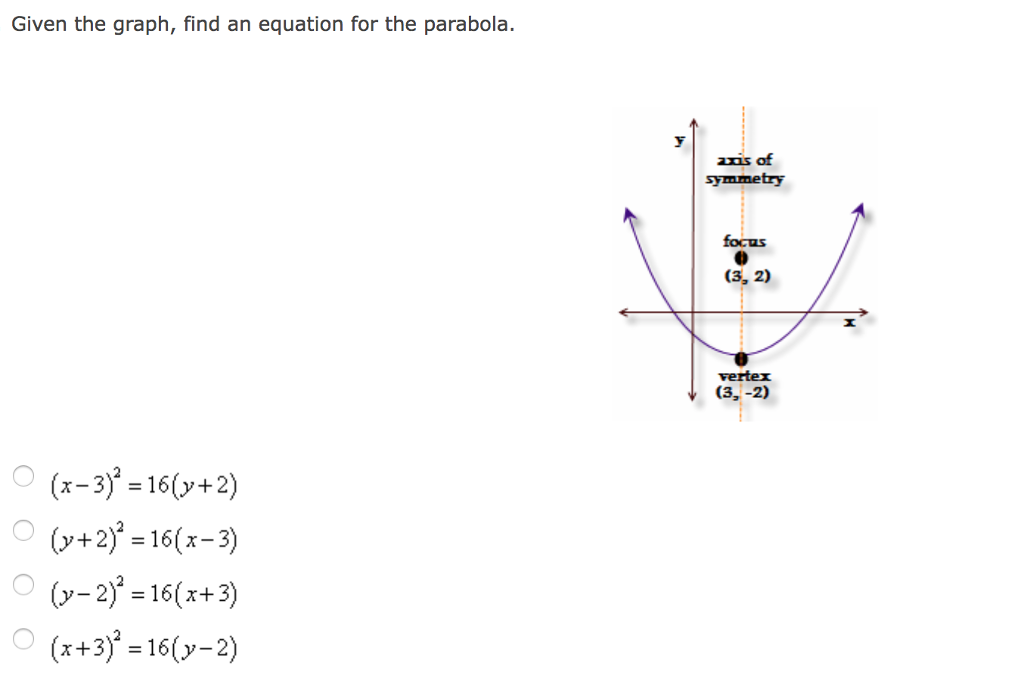



Given The Graph Find An Equation For The Parabola Chegg Com
Equation of the parabola $$$ y=2 x^{2} x 3 $$$ Vertex form $$$ y=2 \left(x \frac{1}{4}\right)^{2} \frac{23}{8} $$$ No intercept form Vertex $$$ \left(\frac{1}{4},\frac{23}{8}\right) $$$ Focus $$$ \left(\frac{1}{4},3\right) $$$ Eccentricity $$$ 1 $$$ Directrix $$$ y=\frac{11}{4} $$$ Latus rectum $$$ y=3 $$$The graph of the equation y = x 2, shown below, is a parabola (Note that this is a quadratic function in standard form with a = 1 and b = c = 0) In the graph, the highest or lowest point of a parabola is the vertex The vertex of the graph of y = x 2 is (0, 0) If a > 0 in f (x) = a x 2 b x c, the parabola opens upward In this case the 2 Answers2 Active Oldest Votes 4 So as StackID just explained in his comprehensive answer, no x → x 3 is not a parabola, and neither is x → x 4, because in terms of polynomials, only second degree polynomials can qualify as a parabola But if what you want to know is actually whether x → x 3 is still a polynomial, that is to
Advanced Math questions and answers X Y^2 = 1with parabola X=3 right the region between X=3 Find the volume of rotation obtained by rotating it about the linX Y^2 = 1with parabola X=3 right the region between X=3 Find the volume of rotation obtained by rotating itVertex\ (y2)=3 (x5)^2 vertex\3x^22x5y6=0 vertex\x=y^2 vertex\ (y3)^2=8 (x5) vertex\ (x3)^2= (y1) parabolafunctionvertexcalculator en 8 janezeshun The vertex of the parabola whose equation is y = (x 1)^2 3 is (1,3) when x = 1,y is the smallest when x = 1 y = (1 1)^2 3 y = 3 Log in for more information Added PM
This is going to be true for all functions, so lets start with a linear equation y = x 3 the y intercept is 3 (set x=0) and the x intercept is 3 (set y = 0) If we keep it as a change in y, we have y = x 3, so it is easy to see the y intercept By "making it a change in x" instead, we show it as y = (x 3The equation of the line passing through the point of intersection of the lines x 3y 2 = 0 and 2x 5y 7 = 0 and perpendicular to the line 3x 2y 5 = 0, is The equation of the line which cuts off the intercepts 2a sec θ and 2a cosec θ on the axes is profile kautzaustin kautzaustin Mathematics High School answer answered The vertex form of the equation of a parabola is y = (x 3)2 36



Graphing Quadratic Functions



Vertex And Intercepts
If a is positive then the parabola opens upwards like a regular "U" (same as standard form) If a is negative, then the graph opens downwards like an upside down "U"(same asFind the yintercept The yintercept of any graph is a point on the yaxis and therefore has xcoordinate 0 We can use this fact to find the yintercepts by simply plugging 0 for x in the original equation and simplifying Notice that if we plug in 0 for x we get y = a(0) 2 b(0) c or y = c So the yintercept of any parabola is always atWe have to find the equation of the parabola which has vertex at ( 0,3 ) If we write the equation of a parabola in the vertex from then we will write y = ( x h )² (k)² In this equation ( h, k) will be the vertex (a) y = (x3)² 0 so ( 3,0) will be the vertex (b) y = ( x3)² 0 or y = x (3)² 0




Ex 11 2 8 Find Equation Of Parabola Focus 0 3 Y 3



Exploration Of Parabolas
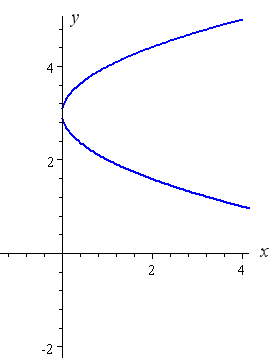
In algebraic geometry, the parabola is generalized by the rational normal curves, which have coordinates (x, x 2, x 3, , x n); Find the length of the common chord of the parabola y^2=4(x3) and the circle x^2y^24x=0 Updated On 246 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!And y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relation




The Equation Of The Directrix Of The Parabola Y 2 4y 4x 2 0 Is




Characteristics Of Parabolas College Algebra
The focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focusSolution Write the equation of parabola in standard form Add 16 to each side (y 4)2 = (x 3) is in the form of (y k)2 = 4a (x h) So, the parabola opens up and symmetric about xaxis with vertex at (h, k) = (3, 4) Divide each side by 4The parabola y 2 = 4 x and x 2 = 4 y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S 1 , S 2 , S 3 are the areas of these parts numbered from top to bottom respectively, then This question has multiple correct options




2 Consider The Quadratic Relationship Y X 3 2 4 Chegg Com



Graphing Quadratic Functions
Algebra Graph y= (x3)^22 y = (x − 3)2 2 y = ( x 3) 2 2 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 3 h = 3 k = 2 k = 2 Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downCalculadora gráfica en línea, gratis e interactiva, de GeoGebra grafica funciones, representa datos, arrastra deslizadores, ¡y mucho más!



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




How To Draw Y 2 X 2
What is the vertex of the parabola y=2(x3) 2 4 Preview this quiz on Quizizz Determine the vertex of the parabola y=5(x2)2–7 Quadratic Functions Vertex Form DRAFT 11th 12th grade 307 times Mathematics 64% average accuracy 3 years ago mrwright16 2 Save Edit EditThe coordinates of end point of the latus rectum of the parabola (y − 1) 2 = 4 (x 1) are View Answer An arch is in the shape of a parabola whose axis is vertically downward and measures 8 0 meters across the bottom on the groundThe center is the same as the center of a circle whose equation is x2 y2 8x 6y 24 = 0 (x 4)2 (y 3)2 = 2² Consider a circle whose equation is x2 y2 2x 8 = 0 Which statements are true?



Solution Graph Y X 2 3 And Y X 3 2 What Are The Similarities And Differences Between The Graphs How Do These Graphs Compare To The Graph Of Y X 2



Quadratics Graphing Parabolas Sparknotes
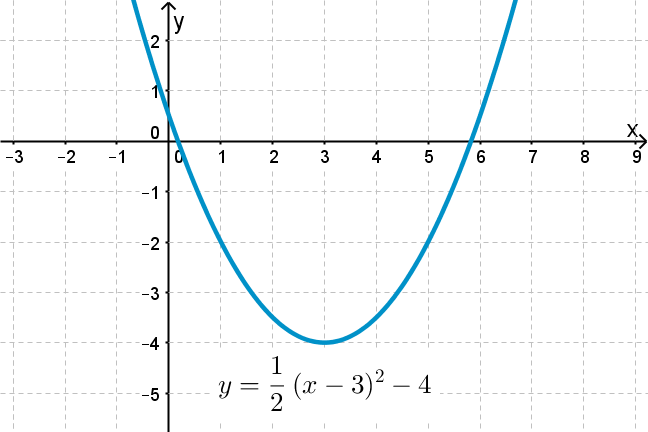
Graphing y = (x h)2 k In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of yYou can put this solution on YOUR website!Create your account View this answer Given The equation of the parabola y = (x−3)2 4 (x−3)2 = (y−4) y = ( x − 3) 2 4 ( x − 3) 2 = ( y − 4) Now compare it See full answer below



A 26 Vertex Form Of A Quadratic Function
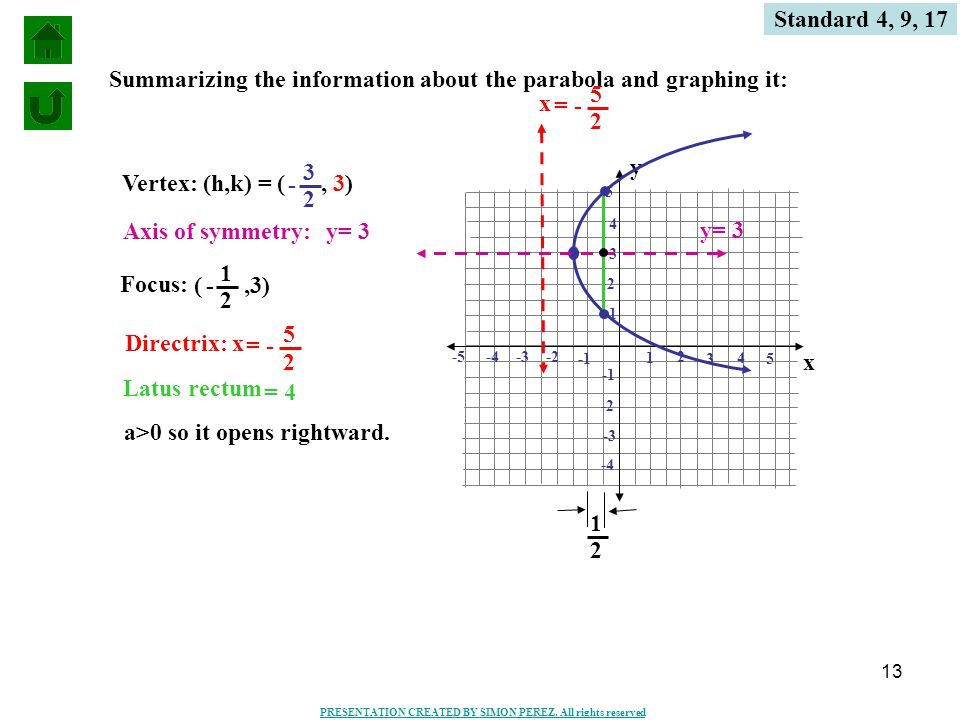



Definition Of A Parabola Ppt Video Online Download
We actually have 2 functions, y = √ x (the top half of the parabola);Watch Video in App This browser does not support the video elementThe standard parabola is the case n = 2, and the case n = 3 is known as the twisted cubic A further generalization is given by the Veronese variety, when there is more than one input variable




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube



Graphing Quadratic Functions
If three points are given we can find A, B and C Similarly, when the axis is parallel to the y – axis, the equation of parabola is y = A'x 2 B'x C' Illustration Find the equation of the parabola whose focus is (3 , 4) and directrix x – y 5 = 0 Solution Let P (x, y) be any point on the parabolaWhat is the following parabola's axis of symmetry of y = x 2 − 2 x − 3 Since this equation is in standard form, use the formula for standard form equation x = − b 2 a Answer the axis of symmetry is the line x = 1 Problem 7Graph the parabola find the vertex y = 2(x 3)(x 1) Multiply using FOIL y = 2(x² x 3x 3) Combine like terms y = 2(x² 2x 3) Distribute to remove parentheses y = 2x² 4x 6 Factor coefficient of x² out of first two terms only y = 2(x² 2x) 6 On scratch paper, multiply the coefficient of x inside the parentheses, which is 2
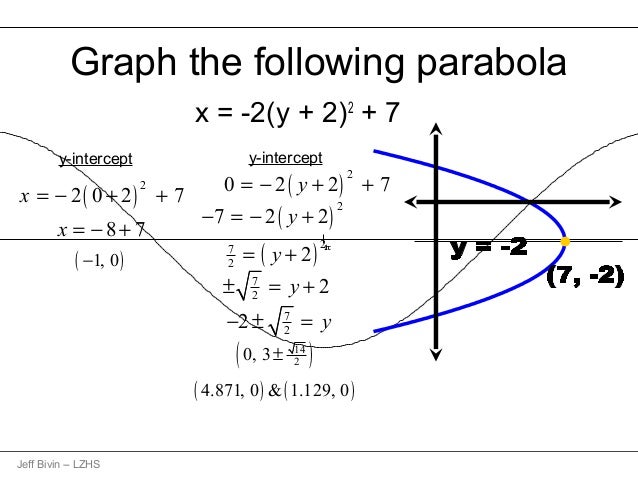



Parabola



Solution Graph The Parabola Y X 4 2 2
The given quadratic equation is in the vertex form y = (x − 3)2 − 2 Hence the vertex is (3, − 2) (3, −2) This is one of the points on the curve x = − 3 is the minimum point on the curve Hence to graph the curve, we take two point to the left of x = 3 and two point to its right Right side points At x = 5;y = (5− 3)2 − 2 = 4 −2 = 2Each of the parabola you drew in (a) y = (x 3)2 (d) Determine the coordinate of the turning points of each of the following quadratics Note that the value of a is irrelevant 10 DO NOW Thursday 1/3 Given the function f(x) — 2x 61 3, state whether the vertex represents aIn this case, the equation of the parabola comes out to be y 2 = 4px where the directrix is the verical line x=p and the focus is at (p,0) If p > 0, the parabola "opens to the right" and if p 0 the parabola "opens to the left" The equations we have just established are known as the standard equations of a parabola A standard equation always




Given The Graph Find An Equation For The Parabola Chegg Com




The Equation Of The Tangent To The Parabola Y X 3 2 Parallel To The Chord Joining The Points 3 0 And 4 1 Is
Key Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;Axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2}4 en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and dedicationY = (1/)x² The equation of the parabola whose focus is at (7, 0) and directrix at x = 7 is x = (1/28)y² The equation of the parabola whose focus is at (3, 0) and directrix x = 3 is y = (1/12)x² x = (1/4)y^2 The focus of the parabola is (1,0) 36y = x^2



Solved A Compare The First Line Of Parabolas With Parent Y X Y X 2 Y X 2 Y X 3 Y X 4 Screenshot Your Graph Of The Parabolas Belo Course Hero




8 2 Graph And Write Equations Of Parabolas Ppt Download
The tangent line to the parabola mathy^2=6x3/math implies math2yy' = 6/math implies mathy' = \frac 3y/math The perpendicular to the line mathx3yY = (x 3) 2 a In the equation above, a is a constant The graph of the equation in the xyplane is a parabola Which of the following is true about the parabola? Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the y intercept y = 12 x 2 48 x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for y y = 12 (0) 2 48 (0



Quadratics Graphing Parabolas Sparknotes
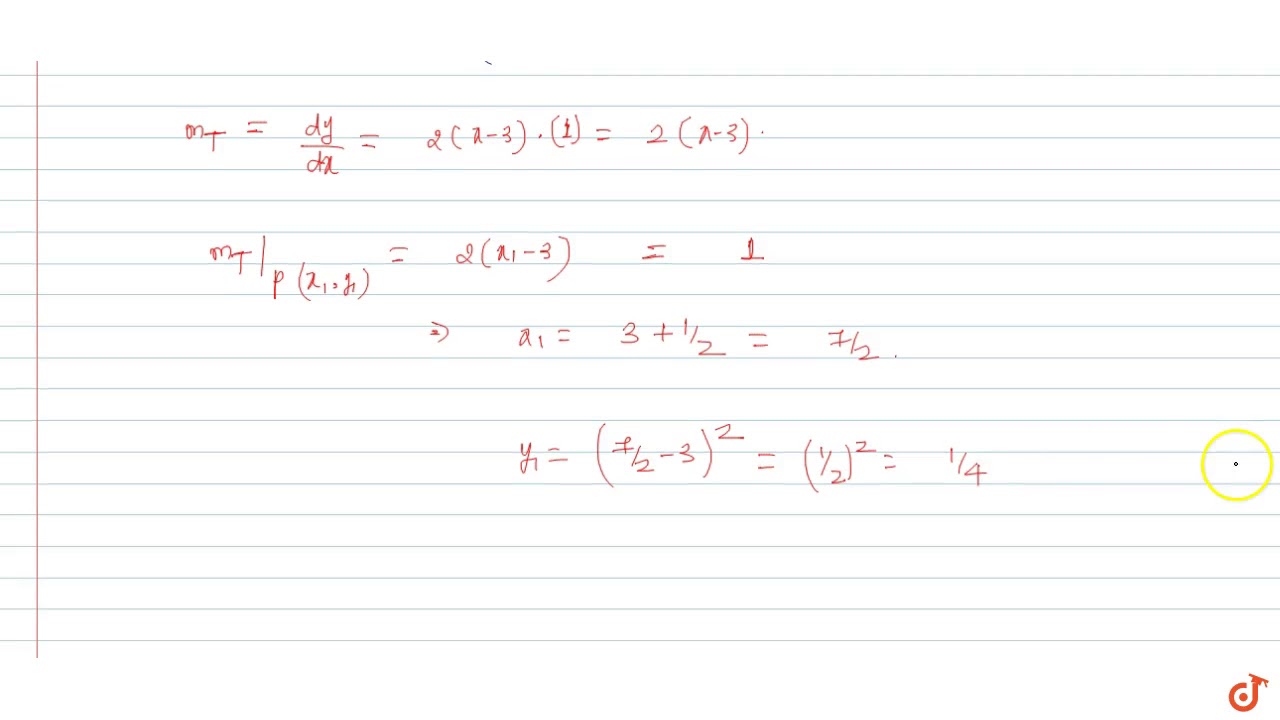



The Equation Of The Tangent To The Parabola Y X 3 2 Parallel To The Chord Joining The Youtube
The vertex form of a parabola's equation is generally expressed as $$ y= a(xh)^ 2 k $$ (h,k) is the vertex;For any parabola, Ax 2 BxC, the x coordinate of the vertex is given by B/(2A) In our case the x coordinate is Plugging into the parabola formula for x we can calculate the y coordinate y = 10 * 300 * 300 60 * 300 10 or y = 8000 Parabola, Graphing Vertex and XIntercepts Root plot for y = x 2 6x1A) Its minimum occurs at (3, a) B) Its minimum occurs at (3, a) C) Its maximum occurs at (3, a) D) Its maximum occurs at (3, a)
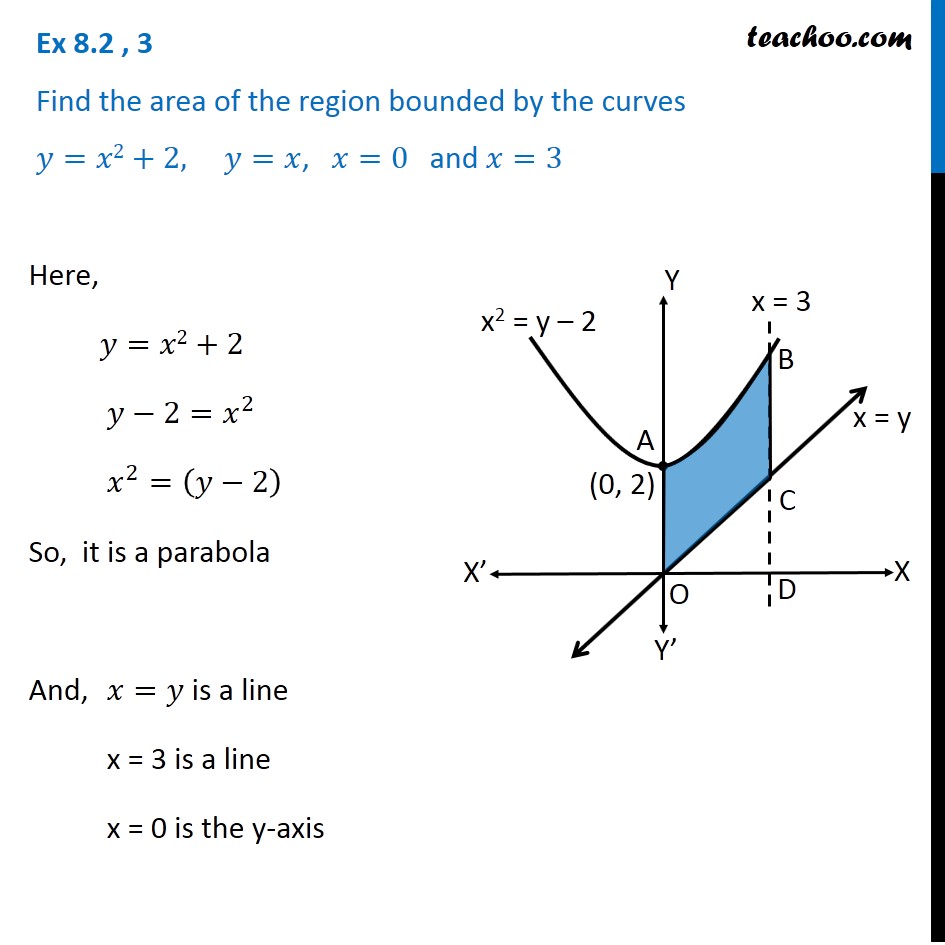



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3




The Vertex Of This Parabola Is At 3 2 Which Of The Following Could Be Its Equation A Brainly Com
The cube of a number or any other mathematical expression is denoted by a superscript 3, for example 2 3 = 8 or (x 1) 3 The cube is also the number multiplied by its square n 3 = n × n 2 = n × n × n The cube function is the function x ↦ x 3 (often denoted y = x 3) that maps a number to its cube It is an odd function, asWhen graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aEje\(y3)^2=8(x5) directriz\(x3)^2=(y1) parabolaequationcalculator es Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowing



Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly




Graphing Parabolas
Mathy=x^2bxc/math What we are really looking for is a value for mathb/math and mathc/math Once we can find those two values, we can simply plug them back into mathy=x^2bxc/math to get the equation of the parabola Let's startGiven data The equation of parabola is {eq}x=y^21{/eq} The equation of line is, {eq}x=3{/eq} The expression of the volume of the solid is expressed as,For example, when we looked at y = (x 3) 2 4, the xcoordinate of the vertex is going be 3;



Solution Find The Equation Of The Line Of Symmetry Of The Parabola Defined By The Equation Y 5x 2 15x 8




Write An Equation For The Following Parabola A X 5 2 5 B X 3 2 4 C X 5 2 4 D X 3 2 5 Brainly Com
Check all that apply The radius of the circle is 3 units The center of the circle lies on the x
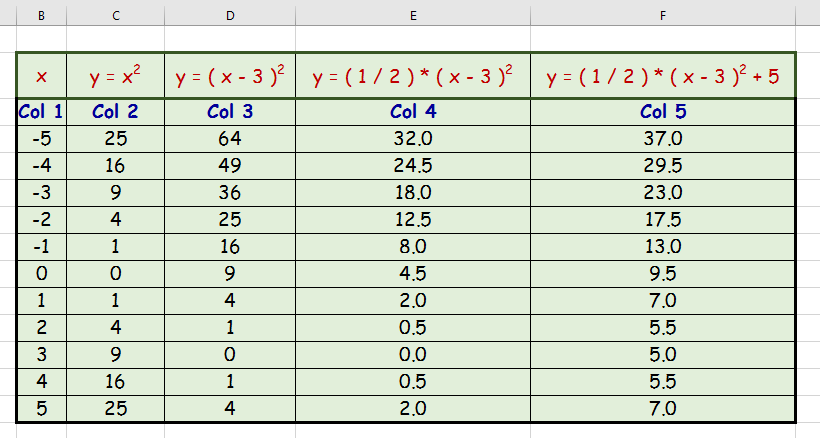



How To Graph A Parabola Y 1 2 X 3 2 5 Socratic



Draw The Graph Of Y X 1 X 3 And Hence Solve X 2 X 6 0 Sarthaks Econnect Largest Online Education Community




Graphing Parabolas




How To Draw Y 2 X 2




Graph A Parabola Whose X Intercepts Are At X 3 And X 5 And Whose Minimum Value Is Y 4 Brainly Com
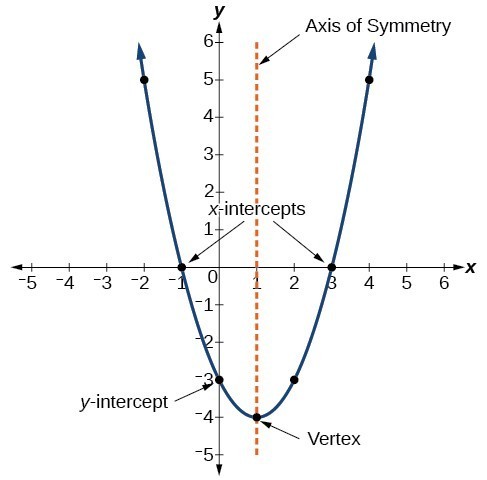



Characteristics Of Parabolas College Algebra




View Question The Graph Of Y 2x 4 X 4 Is A Parabola In The Xy Plane In Which Of The Following Equivalent Expressions Do The X And Y Coordinates Of
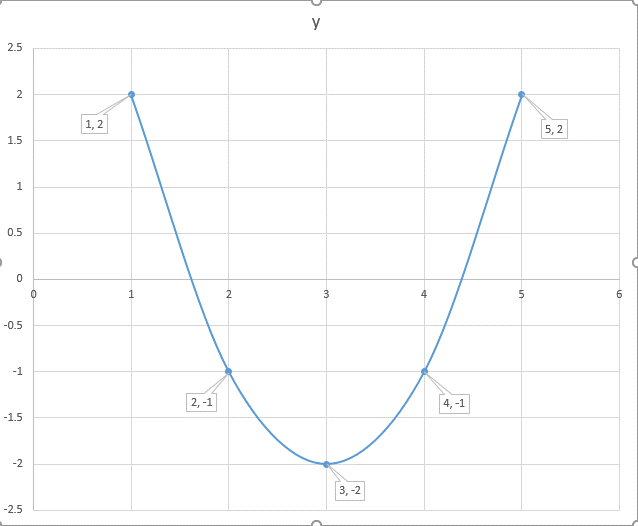



How Do You Graph The Parabola Y X 3 2 2 Using Vertex Intercepts And Additional Points Socratic
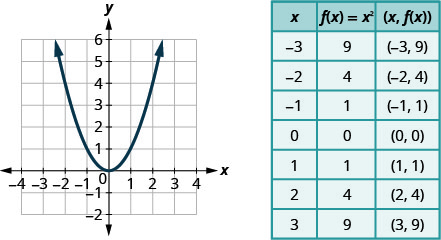



9 7 Graph Quadratic Functions Using Properties Mathematics Libretexts
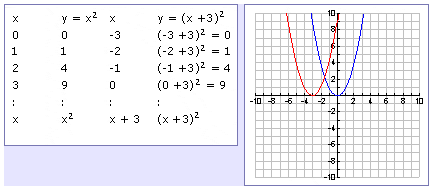



Transformations




Answered Ex 5 Find The Equation Of The Parabola Bartleby



Graphing Quadratic Equations Using Transformations




Quadratic Functions



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com



How To Draw Y 2 X 2




Shifting Parabolas Video Khan Academy



1



Quadratics Graphing Parabolas Sparknotes




Solved Find The Vertex Focus And Directrix Of The Parab Chegg Com



How To Find The Equation In The Standard Form Of A Parabola With Directrix X 1 And Focus 3 2 Quora



Math Spoken Here Classes Quadratic Equations 3



Quadratics Graphing Parabolas Sparknotes




Quadratic Function




Find The Point On The Parabola Y X 3 2 Where The Tangent Is




How To Find The Coordinates Of The Points Of Intersection Of The Parabola Y Xx And Y X 3 Quora




Find The Area Bounded By Curves Y X 2y 3 X And X Axis




10 Find The Focus Of The Parabola Y 1 4 X 3 2 2 A 3 1 B 3 2 C 3 1 D 3 2 Brainly Com



1



Scaling And Translating Quadratic Functions



Solution How To Graph Y X 3



A Parabola Has A Focus At 3 7 And A Directrix Of Y 1 Where Is Its Vertex Quora




Graph The Parabola Y X 3 2 1 Brainly Com



1



Graphing Quadratic Functions




Please Help The Vertex Form Of The Equation Of A Parabola Is Y X 3 2 36 What Is The Standard Brainly Com
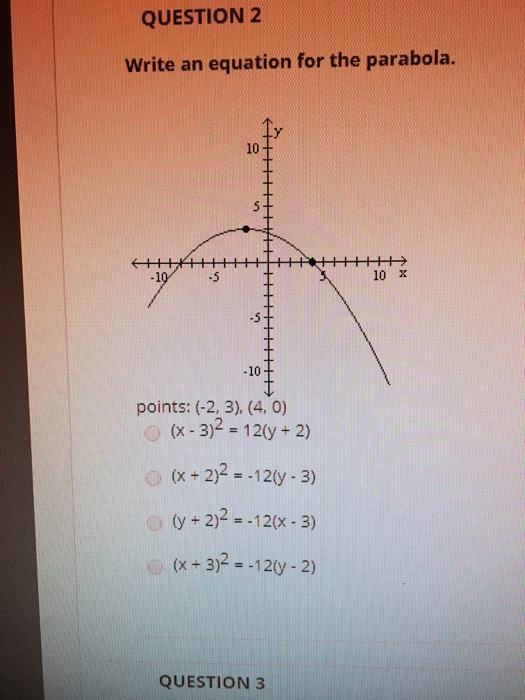



Solved Question 2 Write An Equation For The Parabola 10 Chegg Com
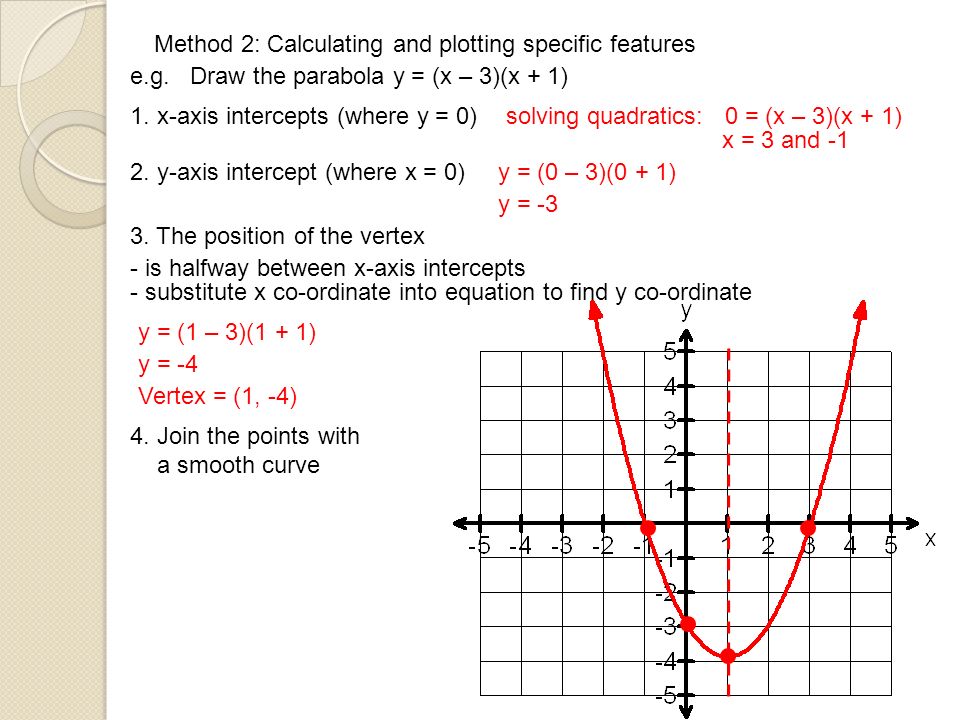



Parabolas Ppt Download




Shifting Parabolas Video Khan Academy
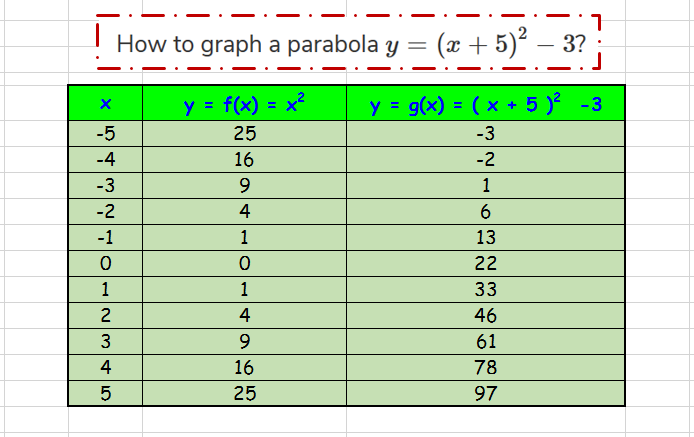



How To Graph A Parabola Y X 5 2 3 Socratic



Quadratics Graphing Parabolas Sparknotes




Answered On The Parabola When The Line Bartleby
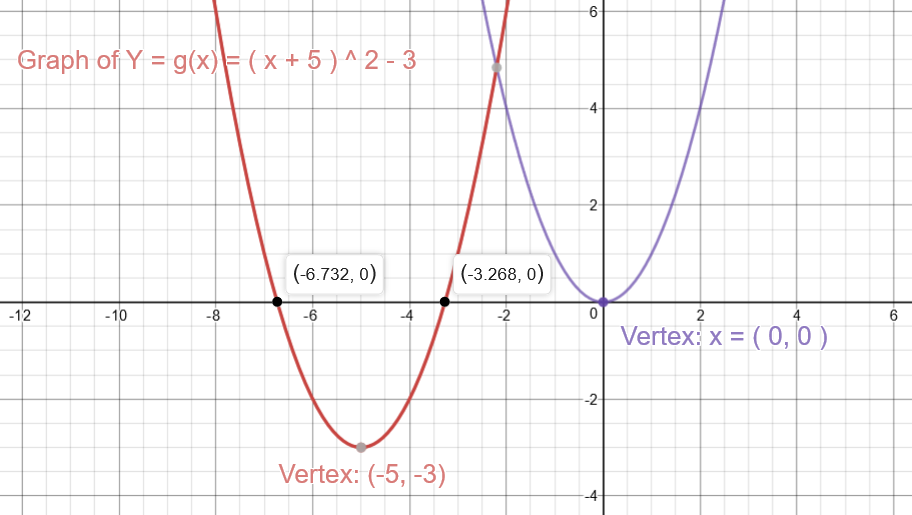



How To Graph A Parabola Y X 5 2 3 Socratic
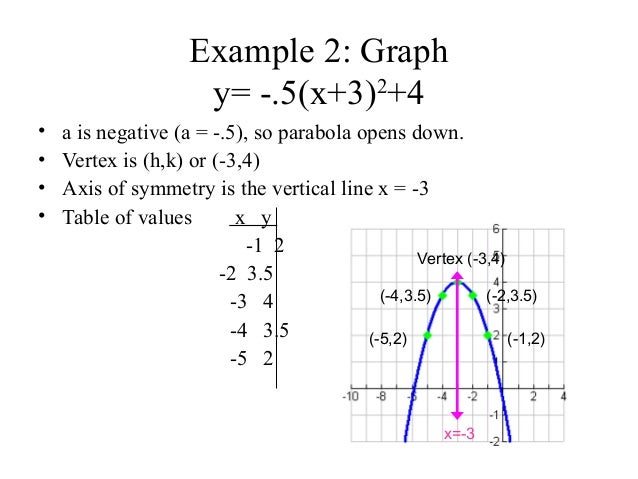



Parabola Complete



What Are The Points Of Intersection Of The Two Parabolas With Equation Y X 3 2 2 And Y X 2 4x 1 Show Your Work Quora




5 3 Translating Parabolas Graphing Vertex Form Y A X H K We Still Look For The Same Things In Vertex Form Happy Or Sad 2where Is The Vertex Ppt Download




Math Lesson 7
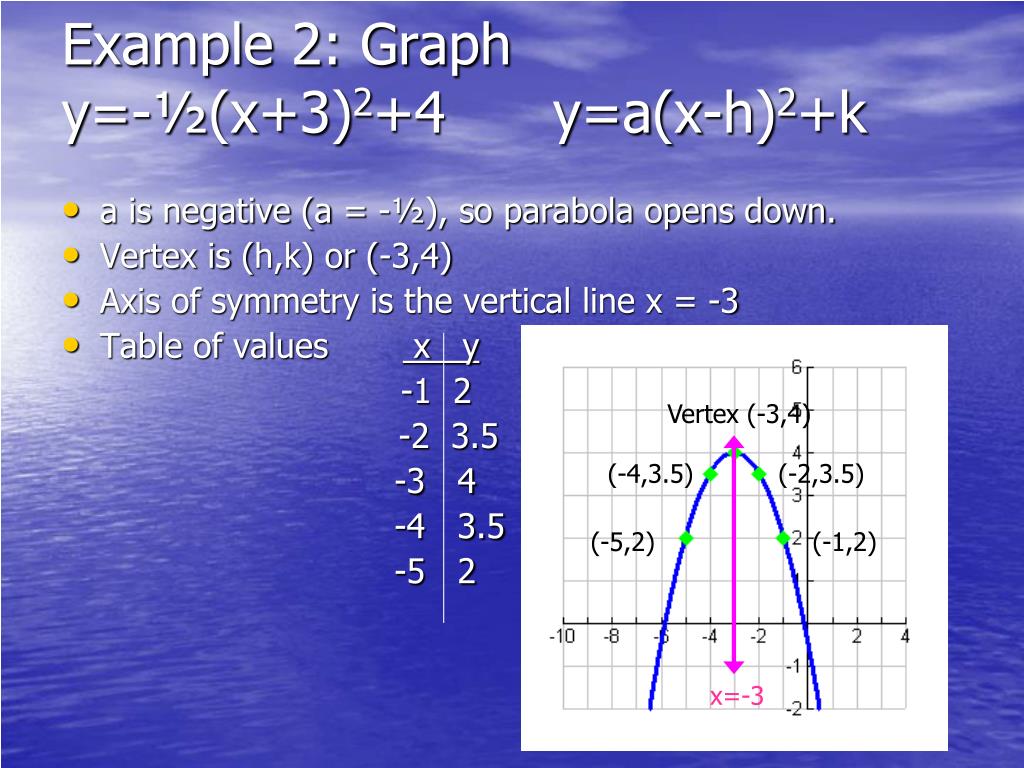



Ppt 1 2 Graphing Quadratic Functions In Vertex Or Intercept Form Powerpoint Presentation Id



Math Spoken Here Classes Quadratic Equations 3
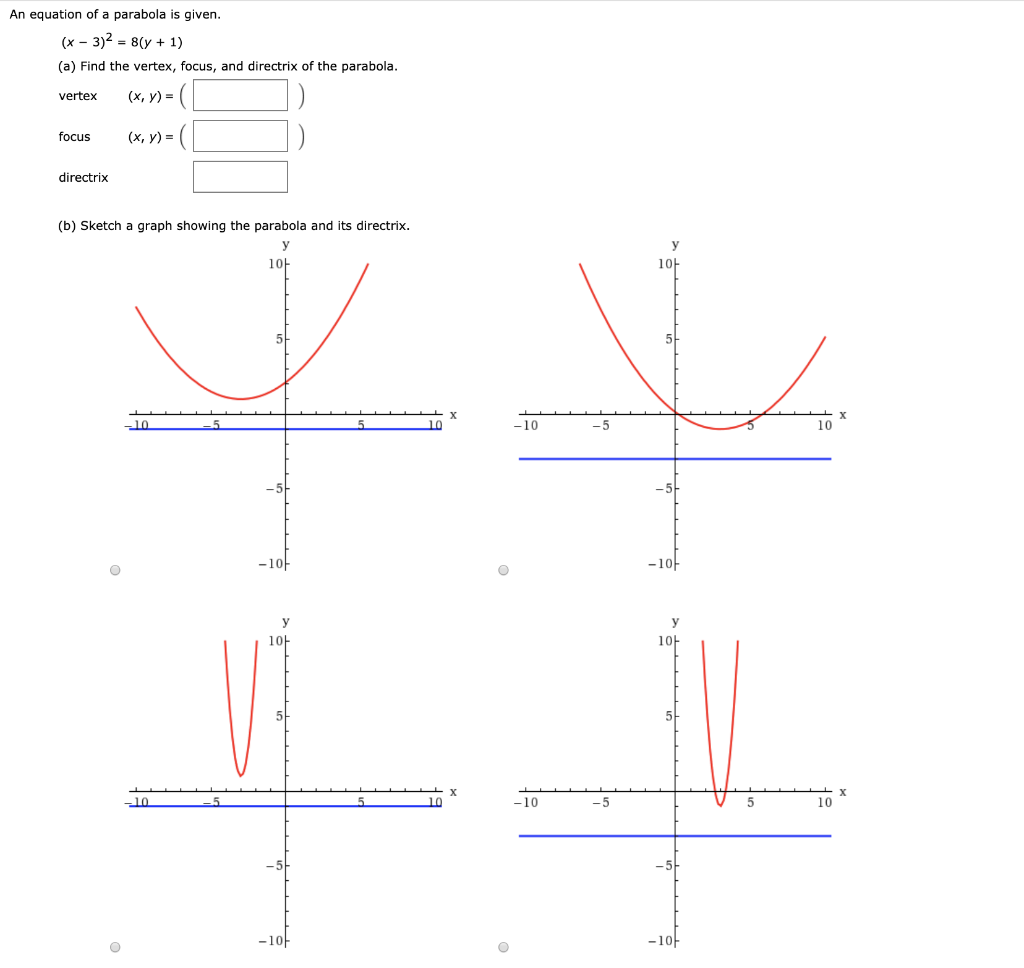



An Equation Of A Parabola Is Given X 3 2 8 Y Chegg Com
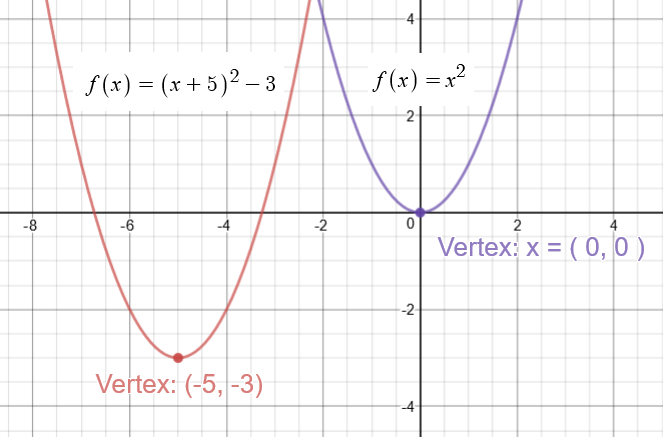



How To Graph A Parabola Y X 5 2 3 Socratic




Content Transformations Of The Parabola



Solution How Do You Graph Y X 3 2 2



Parabolas



Graphing Quadratic Functions
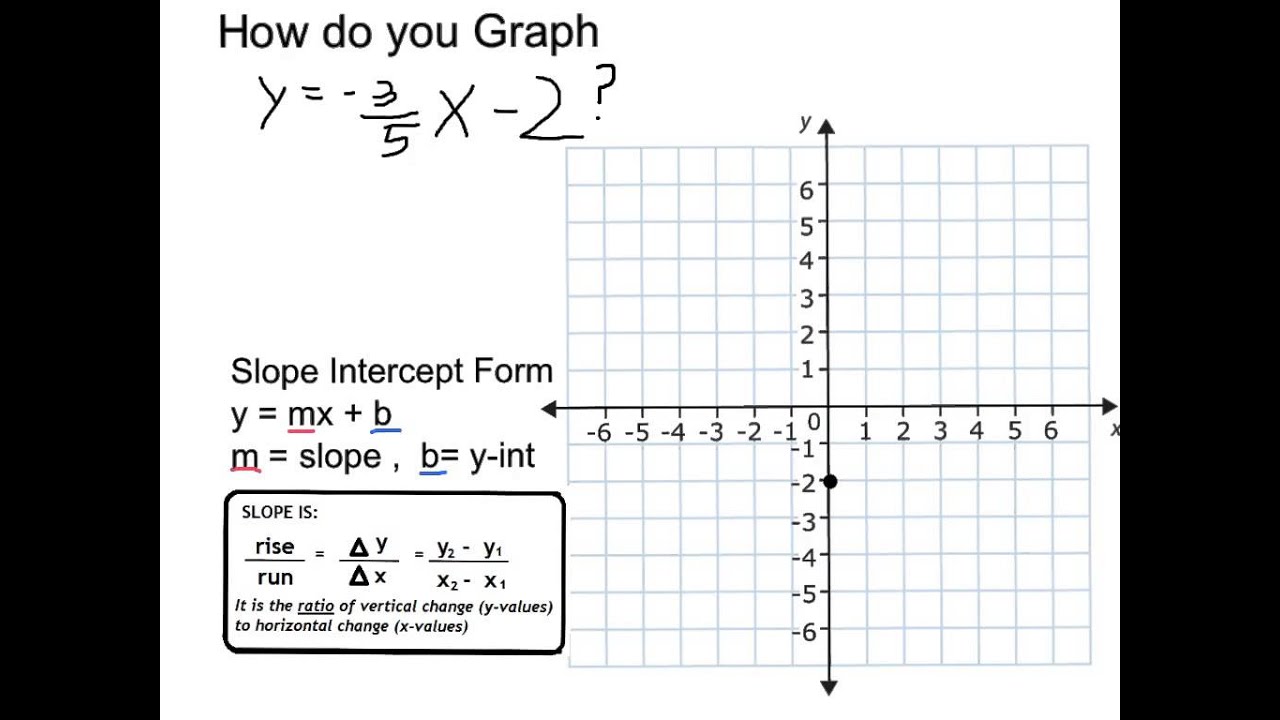



Graph Y 3 5 X 2 Youtube




Graphing Parabolas




4 1 4 3 Review Sketch A Graph Of The Quadratic Y X 3 Find Vertex 3 5 Axis Of Symmetry X 3 Y Intercept 0 4 X Intercepts Ppt Download




Quadratic Function




Focus Of The Parabola Y 2 2 X 3 Is Youtube




Find The Vertex Focus And Directrix Of The Chegg Com



Solution 1 Find The Equation For The Parabola With Focus 3 2 And Directrix Y 6 2 Write The Equation For The Circle With Center 3 4 And Radius 5square Root 2 3 Write The Equa



1
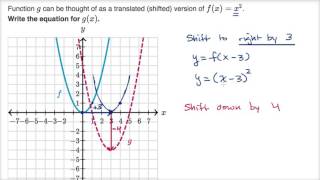



Shifting Parabolas Video Khan Academy




The Vertex Of The Parabola Below Is At The Point 1 3 Which Of The Equations Below Could Be The Brainly Com




Graph A Parabola Whose X Intercepts Are At X 3 And X 5 And Whose Minimum Value Is Y 4 Brainly Com




The Graphs Of X 2 12 Y And X 3 2 12 Y 1 Are Given Label The Focus Directrix And Vertex On Each Parabola Bartleby




Content Transformations Of The Parabola




Graph Y X 2 3 Youtube
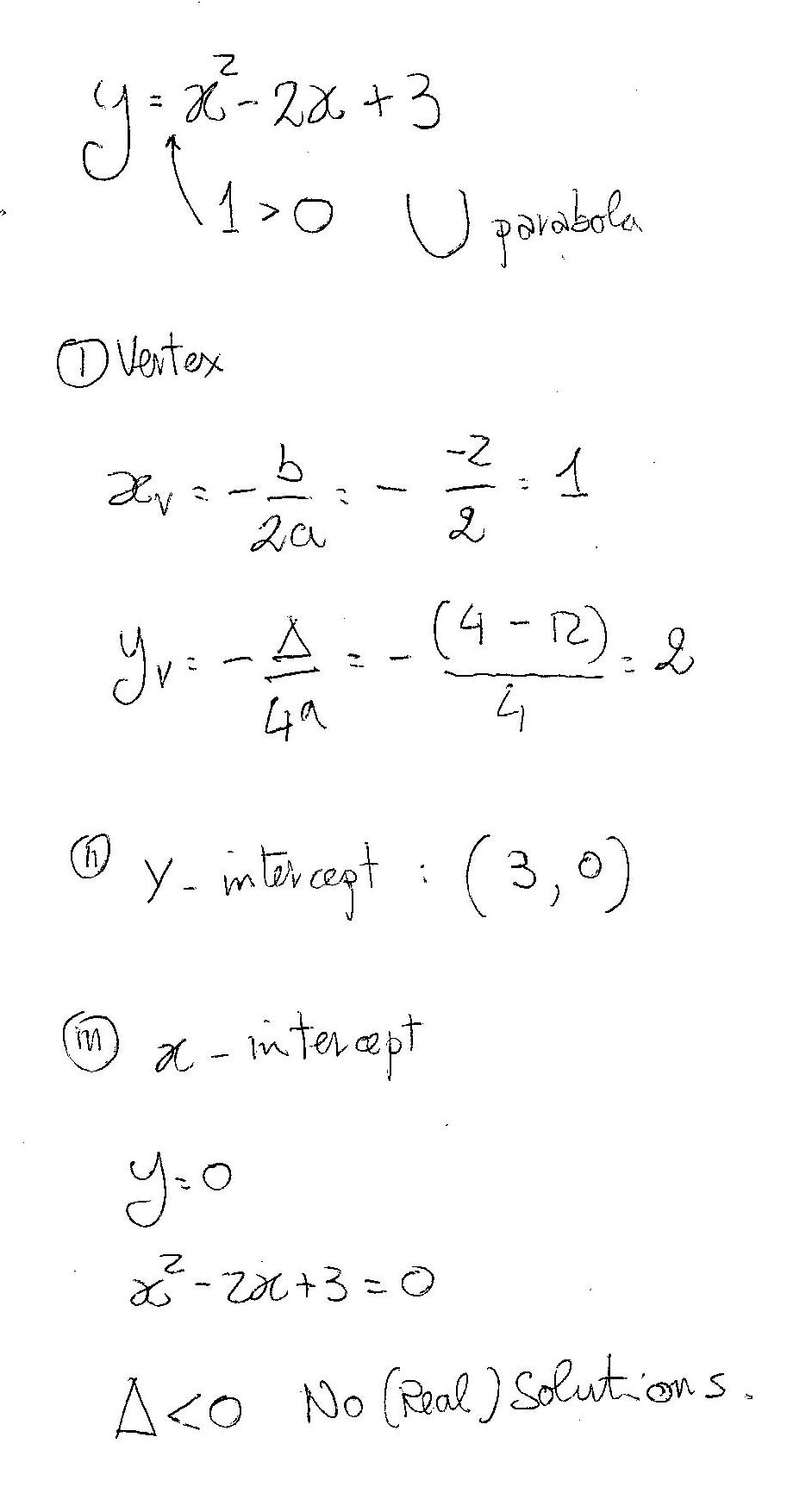



How Do You Graph Y X 2 2x 3 Socratic




Find Two Different Parametric Representations For The Chegg Com
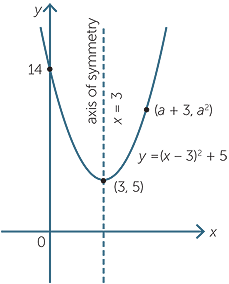



Quadratic Function
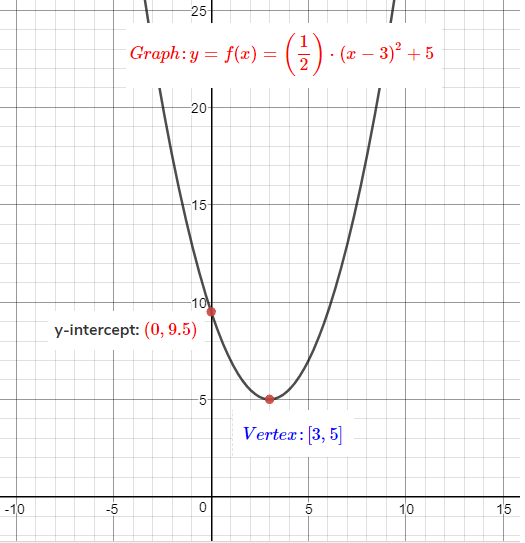



How To Graph A Parabola Y 1 2 X 3 2 5 Socratic



Solution Given The Equation Y X 2 7 Calculate The Corresponding Y Coordinates For X 3 1 0 1 3 Please Show All Of Your Work Plot Those Points And Graph The Equation



An Equation Of A Parabola Is Given 4 X 3 2 Y Chegg Com



0 件のコメント:
コメントを投稿